Genetic Algorithms

What is a Genetic Algorithm?

      Evolutionary computing is a field of computer science in which large, complex tasks are solved by evolving solutions through systematic trial and error. There are several branches of evolutionary computing such as genetic programming and genetic algorithms, the method used in this particular model. A genetic algorithm mimics the Darwinian theory of evolution to evolve solutions to specific problems. A set population of individules with different fitnesses is evolved by selecting two individules through a predetermined method, such as random selection of a small group with only the more fit individules being selected for crossover. The two individuals then combine their information to form an offspring that is similar to its parents. Over time, the genetic algorithm replaces the most unfit individuals with stronger ones.

How Genetic Algorithms Work

      Genetic Algorithms use two functions to introduce genetic variability into a population: crossover and mutation. These are modeled after their real-life genetic counterparts; Crossover works by taking two individuals and switching their genetic information at one or more points in order to form a new individual. The point(s) a which the crossover takes place is called a crossover point.

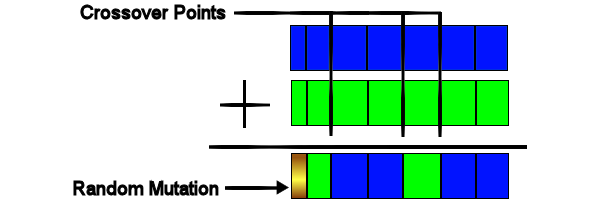
      In the image above there are three(3) different crossover points, so the offspring is made up of four(4) separate fragments from both parents. You can also see that mutation has occurred to the first value in the individual. Both the crossover points and the any mutated individules are selected at random. Mutation is typically less likely to occur than crossover, but it plays an equally important role in improving the overall fitness of the model. Mutation in the genetic algorithm is similar to mutation in nature, where one aspect of an individual is modified slightly. In the GA, an element of the individual is altered in such a way that the change could be potentially large, but in most cases it will only be minute. This ensures that if the fitness of the individual decreases, it will not be such a dramatic loss.

Our Genetic Algorithm

      The arm model used in our research uses one neural network to control each muscle bundle (Click here for an example) . Each network is made up of many different neurons that propagate a signal from the brain to the alpha-motoneuron. The neurons are connected to each other in order to successfully propagate the signal through the network, but because we are using an integrate-and-fire model, a 1:1 connection between each neuron isn't enough to achieve the desired arm movement. Because of this, different weights are placed between the neural connections, which in turn cause the propagated signal's effect to be multiplied by that weight. This particular model uses a 64-bitdouble (basically a really accurate number) that ranges from 0 to 3 inclusive. In order for the model to produce the target movement the weights need to be carefully balanced, and because there are about 600 weights in each model, a genetic algorithm is neccessary to acomplish this task.
      The genetic algorithm used in this particular model uses both crossover and mutation techniques. After each simulation is run the two parents are selected through a 2-way tournament, meaning that two individuals are selected at random and of those two, the one with the best fitness is selected for crossover. Crossover is guaranteed to occur twice every time the weights are tested. This is not necessarily the case with mutation. Each weight is made up of so many digits, and the probability of each digit being mutated is 1/n, where n is the number of digits in the entire number.

	Example:
		-weight = 2.651974624
		-number of digits = 10
		-probability of mutation = 0.1

      This makes it easy to assume that the weight as a whole must be mutated at some point, but it leaves the possibility of no mutation open as well as multiple mutations occurring within the same weight. How much an individual is mutated is based on a Gaussian distribution, where the result of the mutation will be relatively near the original value. The goal of using both crossover and mutation is to quickly reach a good fitness with crossover, and then slowly refine that fitness to be as good as possible with mutation.