The maximum clique problem (MC) is defined as follows:
Given an undirected graph G = (V,E) where V is the set of
vertices
of the graph and E is the set of edges. A clique is a set of
mutually adjacent vertices. I.e. there is an edge between every pair of
vertices in a clique. The maximum clique problem is to find the largest
(hence maximum) clique in a given graph.
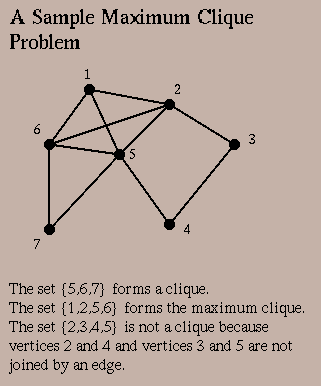
The maximum clique problem is NP-complete. So, it is known to be hard to solve. Further, there are known bounds for approximating MC in polynomial time. That is no approximation technique can promise to find an approximate solution that is better than a known limit in polynomial time. Because the approximation bound is fairly low MC is known to be difficult to approximate and a good candidate for evolutionary computation.
MC also has several practical applications, including coding theory, geometry, and fault diagnosis in large multiprocessor systems. The application depends in part on how the graph was generated. Certain problems lead to graphs with particular characteristics. Thus, it makes sense to test a GA (or any other search technique) on graphs of several different types. For the project you should test at least the following four graphs: c-fat500-1.clq hamming6-2.clq p_hat500-1.clq keller6.clq. keller6.zip. The files storing these graphs begins with a brief description of the graph. The line 'p edge #1 #2' defines the size of the graph: #1 is the number of vertices, #2 is the number of edges. The rest of the file is a list of the edges in the graph (e.g. the line 'e 8 2' means there is an edge between vertex 2 and 8). You will want to save these files and write a function that reads them for your GA to use. Note that solutions to the first 3 graphs have been found. The solutions consist of 14, 32, and 9 vertices respectively. The solutions can be found at dimacs.rutgers.edu/pub/challenge/graph/benchmarks/clique/SOLUTIONS. The solution to Keller6 has not been found, although a clique of size 59 has been found, setting a lower bound on the possible solution size.If you would like to test more graphs, a wide selection is available at the DIMACS challenge web site. This site also describes the signifigance of the different graph types. The graphs are available via anonymous ftp at ftp://dimacs.rutgers.edu in the directory /pub/challenge/graph/benchmarks/clique. To decode the graph files you will need the files bin2asc.c and genbin.h available via anonymous ftp in the directory pub/challenge/graph/translators/binformat/ANSI