Dr. J's Compiler Construction Lecture Notes

Regular Expressions

1. Epsilon (ε) is a regular expression denoting the set containing the empty string
2. Any letter in the alphabet is also a regular expression denoting the set containing a one-letter string consisting of that letter.
3. For regular expressions r and s,
            r | s
   is a regular expression denoting the union of r and s
4. For regular expressions r and s,
            r s
   is a regular expression denoting the set of strings consisting of a member of r followed by a member of s
5. For regular expression r,
            r*
   is a regular expression denoting the set of strings consisting of zero or more occurrences of r.
6. You can parenthesize a regular expression to specify operator precedence (otherwise, alternation is like plus, concatenation is like times, and closure is like exponentiation)

• For regular expression r,
           r+
  is a regular expression denoting the set of strings consisting of one or more occurrences of r. Equivalent to rr*
• For regular expression r,
           r?
  is a regular expression denoting the set of strings consisting of zero or one occurrence of r. Equivalent to r|ε
• The notation [abc] is short for a|b|c. [a-z] is short for a|b|...|z. [^abc] is short for: any character other than a, b, or c.

lecture #3 began here

What is a "lexical attribute" ?

Homework #2

Avoid These Common Bugs in Your Homeworks!

1. yytext or yyinput were not declared global
2. main() does not have its required argc, argv parameters!
3. main() does not call yylex() in a loop or check its return value
4. getc() EOF handling is missing or wrong! check EVERY all to getc() for EOF!
5. opened files not (all) closed! file handle leak!
6. end-of-comment code doesn't check for */
7. yylex() is not doing the file reading
8. yylex() does not skip multiple spaces, mishandles spaces at the front of input, or requires certain spaces in order to function OK
9. extra or bogus output not in assignment spec
10. = instead of ==

Some Regular Expression Examples

What is the regular expression for each of the different lexical items that appear in C programs? How does this compare with another, possibly simpler programming language such as BASIC?

lexical category	BASIC	C
operators	the characters themselves	For operators that are regular expression operators we need mark them with double quotes or backslashes to indicate you mean the character, not the regular expression operator. Note several operators have a common prefix. The lexical analyzer needs to look ahead to tell whether an = is an assignment, or is followed by another = for example.
reserved words	the concatenation of characters; case insensitive	Reserved words are also matched by the regular expression for identifiers, so a disambiguating rule is needed.
identifiers	no _; $ at ends of some; 2 significant letters!?; case insensitive	[a-zA-Z_][a-zA-Z0-9]*
numbers	ints and reals, starting with [0-9]+	0x[0-9a-fA-F]+ etc.
comments	REM.*	C's comments are tricky regexp's
strings	almost ".*"; no escapes	escaped quotes
what else?

lex(1) and flex(1)

The C code generated by lex has the following public interface. Note the use of global variables instead of parameters, and the use of the prefix yy to distinguish scanner names from your program names. This prefix is also used in the YACC parser generator.

FILE *yyin;	/* set this variable prior to calling yylex() */
int yylex();	/* call this function once for each token */
char yytext[];	/* yylex() writes the token's lexeme to an array */
                /* note: with flex, I believe extern declarations must read
                   extern char *yytext;
                 */
int yywrap();   /* called by lex when it hits end-of-file; see below */

The .l file format consists of a mixture of lex syntax and C code fragments. The percent sign (%) is used to signify lex elements. The whole file is divided into three sections separated by %%:

   header
%%
   body
%%
   helper functions

The header consists of C code fragments enclosed in %{ and %} as well as macro definitions consisting of a name and a regular expression denoted by that name. lex macros are invoked explicitly by enclosing the macro name in curly braces. Following are some example lex macros.

letter		[a-zA-Z]
digit		[0-9]
ident		{letter}({letter}|{digit})*

The body consists of of a sequence of regular expressions for different token categories and other lexical entities. Each regular expression can have a C code fragment enclosed in curly braces that executes when that regular expression is matched. For most of the regular expressions this code fragment (also called a semantic action consists of returning an integer that identifies the token category to the rest of the compiler, particularly for use by the parser to check syntax. Some typical regular expressions and semantic actions might include:

" "		{ /* no-op, discard whitespace */ }
{ident}		{ return IDENTIFIER; }
"*"		{ return ASTERISK; }
"."		{ return PERIOD; }

The helper functions in a lex file typically compute lexical attributes, such as the actual integer or string values denoted by literals. One helper function you have to write is yywrap(), which is called when lex hits end of file. If you just want lex to quit, have yywrap() return 1. If your yywrap() switches yyin to a different file and you want lex to continue processing, have yywrap() return 0. The lex or flex library (-ll or -lfl) have default yywrap() function which return a 1, and flex has the directive %option noyywrap which allows you to skip writing this function.

A Short Comment on Lexing C Reals

([0-9]+.[0-9]* | [0-9]*.[0-9]+) ...

([0-9]*.[0-9]*)    { return (strcmp(yytext,".")) ? REAL : PERIOD; }

Lex extended regular expressions

c

normal characters mean themselves

\c

backslash escapes remove the meaning from most operator characters. Inside character sets and quotes, backslash performs C-style escapes.

"s"

Double quotes mean to match the C string given as itself. This is particularly useful for multi-byte operators and may be more readable than using backslash multiple times.

[s]

This character set operator matches any one character among those in s.

[^s]

A negated-set matches any one character not among those in s.

.

The dot operator matches any one character except newline: [^\n]

r*

match r 0 or more times.

r+

match r 1 or more times.

r?

match r 0 or 1 time.

r{m,n}

match r between m and n times.

r₁r₂

concatenation. match r₁ followed by r₂

r₁|r₂

alternation. match r₁ or r₂

(r)

parentheses specify precedence but do not match anything

r₁/r₂

lookahead. match r₁ when r₂ follows, without consuming r₂

^r

match r only when it occurs at the beginning of a line

r$

match r only when it occurs at the end of a line

lecture #4 began here

Announcements

Lexical Attributes and Token Objects

struct token {
   int category;
   char *text;
   int linenumber;
   int column;
   char *filename;
   union literal value;
}

Flex Manpage Examplefest

It turns out the flex man page is intended to be pretty complete, enough so that we can draw our examples from it. Perhaps what you should figure out from these examples is that flex is actually... flexible. The first several examples use flex as a filter from standard input to standard output.

• sneaky string removal tool:

             %%
             "zap me"
  

• excess whitespace trimmer

             %%
             [ \t]+        putchar( ' ' );
             [ \t]+$       /* ignore this token */
  

• sneaky string substitution tool:

             %%
             username    printf( "%s", getlogin() );
  

• Line Counter/Word Counter

                     int num_lines = 0, num_chars = 0;
  
             %%
             \n      ++num_lines; ++num_chars;
             .       ++num_chars;
  
             %%
             main()
                     {
                     yylex();
                     printf( "# of lines = %d, # of chars = %d\n",
                             num_lines, num_chars );
                     }
  

• Toy compiler example

             /* scanner for a toy Pascal-like language */
  
             %{
             /* need this for the call to atof() below */
             #include <math.h>
             %}
  
             DIGIT    [0-9]
             ID       [a-z][a-z0-9]*
  
             %%
  
             {DIGIT}+    {
                         printf( "An integer: %s (%d)\n", yytext,
                                 atoi( yytext ) );
                         }
  
             {DIGIT}+"."{DIGIT}*        {
                         printf( "A float: %s (%g)\n", yytext,
                                 atof( yytext ) );
                         }
  
             if|then|begin|end|procedure|function        {
                         printf( "A keyword: %s\n", yytext );
                         }
  
             {ID}        printf( "An identifier: %s\n", yytext );
  
             "+"|"-"|"*"|"/"   printf( "An operator: %s\n", yytext );
  
             "{"[^}\n]*"}"     /* eat up one-line comments */
  
             [ \t\n]+          /* eat up whitespace */
  
             .           printf( "Unrecognized character: %s\n", yytext );
  
             %%
  
             main( argc, argv )
             int argc;
             char **argv;
                 {
                 ++argv, --argc;  /* skip over program name */
                 if ( argc > 0 )
                         yyin = fopen( argv[0], "r" );
                 else
                         yyin = stdin;
  
                 yylex();
                 }
  

On the use of character sets (square brackets) in lex and similar tools

   COMMENT [/*][[^*/]*[*]*]]*[*/]

lecture #5 began here

Finite Automata A finite automaton (FA) is an abstract, mathematical machine, also known as a finite state machine, with the following components:

1. A set of states S
2. A set of input symbols E (the alphabet)
3. A transition function move(state, symbol) : new state(s)
4. A start state S0
5. A set of final states F

   while ((c=getchar()) != EOF) S := move(S, c);

DFAs

S = {s0, s1, s2}
E = {a, b, c}
move = { (s0,a):s1; (s1,b):s2; (s2,c):s2 }
S0 = s0
F = {s2}

Finite automata correspond in a 1:1 relationship to transition diagrams; from any transition diagram one can write down the formal automaton in terms of items #1-#5 above, and vice versa. To draw the transition diagram for a finite automaton:

• draw a circle for each state s in S; put a label inside the circles to identify each state by number or name
• draw an arrow between S_i and S_j, labeled with x whenever the transition says to move(S_i, x) : S_j
• draw a "wedgie" into the start state S0 to identify it
• draw a second circle inside each of the final states in F

The Automaton Game

DFA Implementation

state := S0
for(;;)
   switch (state) {
   case 0: 
      switch (input) {
         'a': state = 1; input = getchar(); break;
         'b': input = getchar(); break;
	 default: printf("dfa error\n"); exit(1);
         }
   case 1: 
      switch (input) {
         EOF: printf("accept\n"); exit(0);
	 default: printf("dfa error\n"); exit(1);
         }
      }

Deterministic Finite Automata Examples

C Comments:

Nondeterministic Finite Automata (NFA's)

Fortunately, one can prove that for any NFA, there is an equivalent DFA. They are just a notational convenience. So, finite automata help us get from a set of regular expressions to a computer program that recognizes them efficiently.

NFA Examples

multiple transitions on the same symbol handle common prefixes:

factoring may optimize the number of states. Is this picture OK/correct?

C Pointers, malloc, and your future

• Draw "memory box" pictures of your variables. Pencil and paper understanding of memory leads to correct running programs.
• Always initialize local pointer variables. Consider this code:

  void f() {
     int i = 0;
     struct tokenlist *current, *head;
     ...
     foo(current)
  }
  

  Here, current is passed in as a parameter to foo, but it is a pointer that hasn't been pointed at anything. I cannot tell you how many times I personally have written bugs myself or fixed bugs in student code, caused by reading or writing to pointers that weren't pointing at anything in particular. Local variables that weren't initialized point at random garbage. If you are lucky this is a coredump, but you might not be lucky, you might not find out where the mistake was, you might just get a wrong answer. This can all be fixed by

     struct tokenlist *current = NULL, *head = NULL;
  

• Avoid this common C bug:

  struct token *t = (struct token *)malloc(sizeof(struct token *)));
  

  This compiles, but causes coredumps during program execution. Why?
• Check your malloc() return value to be sure it is not NULL. Sure, modern programs will "never run out of memory". Wrong. malloc() can return NULL even on big machines. Operating systems often place limits on memory so as to protect themselves from runaway programs or hacker attacks.

Regular expression examples

(a|c)*b(a|c)*

(a|c)*|(a|c)*b(a|c)*

(a|c)*(b|ε)(a|c)*

Regular expressions can be converted automatically to NFA's

1. For ε, draw two states with a single ε transition.
   
2. For any letter in the alphabet, draw two states with a single transition labeled with that letter.
   
3. For regular expressions r and s, draw r | s by adding a new start state with ε transitions to the start states of r and s, and a new final state with ε transitions from each final state in r and s.
   
4. For regular expressions r and s, draw rs by adding ε transitions from the final states of r to the start state of s.
   
5. For regular expression r, draw r* by adding new start and final states, and ε transitions
   • from the start state to the final state,
   • from the final state back to the start state,
   • from the new start to the old start and from the old final states to the new final state.
   
   
6. For parenthesized regular expression (r) you can use the NFA for r.

lecture #6 began here

NFA's can be converted automatically to DFA's

Operations to keep track of sets of NFA states:

ε_closure(s)

set of states reachable from state s via ε

ε_closure(T)

set of states reachable from any state in set T via ε

move(T,a)

set of states to which there is an NFA transition from states in T on symbol a

NFA to DFA Algorithm:

Dstates := {ε_closure(start_state)}
while T := unmarked_member(Dstates) do {
	mark(T)
	for each input symbol a do {
		U := ε_closure(move(T,a))
		if not member(Dstates, U) then
			insert(Dstates, U)
		Dtran[T,a] := U
	}
}

Practice converting NFA to DFA

...







...did you get:

OK, how about this one:

lecture #7 began here

Some Remarks

• I have a collection of compiler textbooks in my office, which I will make avaliable as "loaners" from class period to class period, all you have to do is sign a return contract in blood.
• If you checked out the class web page, you saw a solution to HW#1 was posted awhile ago... I will try to do this for future assignments also, but not immediately, so as to allow students a few days of lateness without a heavy penalty.
• Whether we return the same or a different category for integer constants and for line numbers depends very much on the grammar we use to parse our language.

Lexical Analysis and the Literal Table

• Efficient storage is necessary to handle large input files.
• There is a colossal amount of duplication in lexical data: variable names, strings and other literal values duplicate frequently
• What token type to use may depend on previous declarations.

A hash table or other efficient data structure can avoid this duplication. The software engineering design pattern to use is called the "flyweight".

Major Data Structures in a Compiler

token

contains an integer category, lexeme, line #, column #, filename... We could build these into a link list, but instead we'll use them as leaves in a tree structure.

syntax tree

contains grammar information about a sequence of related tokens. leaves contain lexical information (tokens). internal nodes contain grammar rules and pointers to tokens or other tree nodes.

symbol table

contains variable names, types, and information needed to generate code for a name (such as its address, or constant value). Look ups are by name, so we'll need a hash table.

intermediate & final code

We'll need link lists or similar structures to hold sequences of machine instructions

Literal Table: Usage Example

%{
/* #define's for token categories LT, LE, etc.
%}

white	[ \t\n]+
digit   [0-9]
id	[a-zA-Z_][a-zA-Z_0-9]*
num     {digit}+(\.{digit}+)?

%%

{ws}	{ /* discard */ }
if	{ return IF; }
then	{ return THEN; }
else	{ return ELSE; }
{id}	{ yylval.id = install_id(); return ID; }
{num}   { yylval.num = install_num(); return NUMBER; }
"<"	{ yylval.op = LT; return RELOP; }
">"	{ yylval.op = GT; return RELOP; }

%%

install_id()
{
   /* insert yytext into the literal table */
}

install_num()
{
   /* insert (binary number corresponding to?) yytext into the literal table */
}

lecture #8 began here

Constructing your Token inside yylex()

Context Free Grammars

• A set of terminal symbols, T
• A set of nonterminal symbols, N
• A start symbol, s, which is a member of N
• A set of production rules of the form A -> w, where A is a nonterminal and w is a string of terminal and nonterminal symbols.

let X = the start symbol s
while there is some nonterminal Y in X do
   apply any one production rule using Y, e.g. Y -> w

Context Free Grammar Examples

lecture #9 began here

Grammar Ambiguity

E -> E + E
E -> E * E
E -> ( E )
E -> ident

E -> E + T
E -> T
T -> T * F
T -> F
F -> ( E )
F -> ident

How can a program figure that x + y * z is legal?
How can a program figure out that x + y (* z) is illegal?

A brief aside on casting your mallocs

#include <stdlib.h>

union lexval *l = (union lexval *)malloc(sizeof(union lexval));

Recursive Descent Parsing

• Write 1 procedure per nonterminal rule
• Within each procedure, a) match terminals at appropriate positions, and b) call procedures for non-terminals.
• Pitfalls:
  1. left recursion is FATAL
  2. must distinguish between several production rules, or potentially, one has to try all of them via backtracking.

Recursive Descent Parsing Example #1

int F()
{
   int t = yylex();
   if (t == IDENT) return 6;
   else if (t == LP) {
      if (E() && (yylex()==RP) return 5;
      }
   return 0;
}

Comment #2: in a real compiler we need more than "yes it parsed" or "no it didn't": we need a parse tree if it succeeds, and we need a useful error message if it didn't.

Question: for E() and T(), how do we know which production rule to try? Option A: just blindly try each one in turn. Option B: look at the first (current) token, only try those rules that start with that token (1 character lookahead). If you are lucky, that one character will uniquely select a production rule. If that is always true through the whole grammar, no backtracking is needed.

Question: how do we know which rules start with whatever token we are looking at? Can anyone suggest a solution, or are we stuck?

lecture #10 began here

Announcements

• Homework #3 minor extension
• Midterm exam: Thursday March 16
• The first midterm exam will cover lexical analysis and syntax analysis

Removing Left Recursion

E -> E + T | T
T -> T * F | F
F -> ( E ) | ident

E  -> T E'
E' -> + T E' | ε
T  -> F T'
T' -> * F T' | ε
F  -> ( E ) | ident

for i := 1 to n do
   for j := 1 to i-1 do begin
      replace each Ai -> Aj gamma with productions
      Ai -> delta1gamma | delta2gamma
      end
   eliminate immediate left recursion

Removing Left Recursion, part 2

case 1: trivial

A : A α | β

A : &beta A'
A' : &alpha A' | ε

E : E op T | T

E : T E'
E' : op T E' | ε

case 2: non-trivial, but immediate

A : A α1 | A α2 | ... | β1 | β2

A :  β1 A' | β2 A' | ...
A' : α1 A' | α2 A' | ... | ε

case 3: mutual recursion

1. Order the nonterminals in some order 1 to N.
2. Rewrite production rules to eliminate all nonterminals in leftmost positions that refer to a "previous" nonterminal. When finished, all productions' right hand symbols start with a terminal or a nonterminal that is numbered equal or higher than the nonterminal no the left hand side.
3. Eliminate the direct left recusion as per cases 1-2.

Left Recursion Versus Right Recursion: When does it Matter?

E : T + E | T - E | T

Recursive Descent Parsing Example #2

S -> A B C
A -> a A
A -> ε
B -> b
C -> c

procedure S()
  if A() & B() & C() then succeed # matched S, we win
end

procedure A()
  if yychar == a then { # use production 2
     yychar := scan()
     return A()
     }
  else
     succeed # production rule 3, match ε
end

procedure B()
   if yychar == b then {
      yychar := scan()
      succeed
      }
   else fail
end

procedure C()
   if yychar == c then {
      yychar := scan()
      succeed
      }
   else fail
end

Backtracking?

S -> cAd
A -> ab
A -> a

S -> cAd
A -> a A'
A'-> b
A'-> (ε)

S -> if E then S
S -> if E then S1 else S2

S -> if E then S S'
S'-> else S2 | ε

Some More Parsing Theory

First(a)

1. First(X) starts with the empty set.
2. if X is a terminal, First(X) is {X}.
3. if X -> ε is a production, add ε to First(X).
4. if X is a non-terminal and X -> Y₁ Y₂ ... Y_k is a production, add First(Y₁) to First(X).

5. for (i = 1; if Yi can derive ε; i++)
           add First(Yi+1) to First(X)
   

First(a) examples

Last time we looked at an example with E, T, and F, and + and *. The first-set computation was not too exciting and we need more examples.

stmt : if-stmt | OTHER
if-stmt:  IF LP expr RP stmt else-part
else-part: ELSE stmt | ε
expr: IDENT | INTLIT

Follow(A)

1. Add $ to Follow(S)
2. if A -> aBb then add First(b) - ε to Follow(B)
3. if A -> aB or A -> aBb where ε is in First(b), then add Follow(A) to Follow(B).

On resizing arrays in C

The problem can be summarized as: step through yytext, copying each piece out to sval, removing doublequotes and plusses between the pieces, and evaluating CHR$() constants.

Space allocated with malloc() can be increased in size by realloc(). realloc() is awesome. But, it COPIES and MOVES the old chunk of space you had to the new, resized chunk of space, and frees the old space, so you had better not have any other pointers pointing at that space if you realloc(), and you have to update your pointer to point at the new location realloc() returns.

i = 0; j = 0;
while (yytext[i] != '\0') {
   if (yytext[i] == '\"') {
      /* copy string into sval */
      i++;
      while (yytext[i] != '\"') {
         sval[j++] = yytext[i++];
         }
      }
   else if ((yytext[i] == 'C') || (yytext[i] == 'c')) {
      /* handle CHR$(...) */
      i += 5;
      k = atoi(yytext + i);
      sval[j++] = k;           /* might check for 0-255 */
      while (yytext[i] != ')') i++;
      }
   /* else we can just skip it */
   i++;
}
sval[j] = '\0'; /* NUL-terminate our string */

• Solution #1: sval = malloc(strlen(yytext)+1) is very safe, but wastes space.
• Solution #2: you could malloc a small amount and grow the array as needed.

  sval = strdup("");
  ...
  sval = appendstring(sval, yytext[i]); /* instead of sval[j++] = yytext[i] */
  

  where the function appendstring could be:

  char *appendstring(char *s, char c)
  {
      i = strlen(s);
      s = realloc(s, i+2);
      s[i] = c;
      s[i+1] = '\0';
      return s;
  }
  

  Note: it is very inefficient to grow your array one character at a time; in real life people grow arrays in large chunks at a time.
• Solution #3: use solution one and then shrink your array when you find out how big it actually needs to be.

  sval = malloc(strlen(yytext)+1);
  /* ... do the code copying into sval; be sure to NUL-terminate */
  sval = realloc(sval, strlen(sval)+1);
  

lecture #11 began here

YACC

YACC files end in .y and take the form

declarations
%%
grammar
%%
subroutines

%token a

declares terminal symbol a; YACC can generate a set of #define's that map these symbols onto integers, in a y.tab.h file. Note: don't #include your y.tab.h file from your grammar .y file, YACC generates the same definitions and declarations directly in the .c file, and including the .tab.h file will cause duplication errors.

%start A

specifies the start symbol for the grammar (defaults to nonterminal on left side of the first production rule).

The grammar gives the production rules, interspersed with program code fragments called semantic actions that let the programmer do what's desired when the grammar productions are reduced. They follow the syntax

A : body ;

Bottom Up Parsing

Example. For the grammar

(1)	S->aABe
(2)	A->Abc
(3)	A->b
(4)	B->d

abbcde
aAbcde
aAde
aABe
S

Handles

1. matches a right hand side of a production rule in the grammar and
2. whose reduction to the nonterminal on the left hand side of that grammar rule is a step along the reverse of a rightmost derivation.

Stack					Input
$						w$

1. Shift one symbol from the input onto the parse stack
2. Reduce one handle on the top of the parse stack. The symbols from the right hand side of a grammar rule are popped of the stack, and the nonterminal symbol is pushed on the stack in their place.
3. Accept is the operation performed when the start symbol is alone on the parse stack and the input is empty.
4. Error actions occur when no successful parse is possible.

The YACC Value Stack

• YACC's parse stack contains only "states"
• YACC maintains a parallel set of values
• $ is used in semantic actions to name elements on the value stack
• $$ denotes the value associated with the LHS (nonterminal) symbol
• $n denotes the value associated with RHS symbol at position n.
• Value stack typically used to construct the parse tree
• Typical rule with semantic action: A : b C d { $$ = tree(R,3,$1,$2,$3); }
• The default value stack is an array of integers
• The value stack can hold arbitrary values in an array of unions
• The union type is declared with %union and is named YYSTYPE

Getting Lex and Yacc to talk

You can either declare that struct token may appear in the %union, and put a mixture of struct node and struct token on the value stack, or you can allocate a "leaf" tree node, and point it at your struct token. Or you can use a tree type that allows tokens to include their lexical information directly in the tree nodes. If you have more than one %union type possible, be prepared to see type conflicts and to declare the types of all your nonterminals.

Getting all this straight takes some time; you can plan on it. Your best bet is to draw pictures of how you want the trees to look, and then make the code match the pictures. No pictures == "Dr. J will ask to see your pictures and not be able to help if you can't describe your trees."

Declaring value stack types for terminal and nonterminal symbols

Example: in the cocogram.y that I gave you we could add a %union declaration with a union member named treenode:

%union {
  nodeptr treenode;
}

%type < treenode > function_definition

%token < tokenptr > SEMICOL

Announcements

lecture #12 began here

Announcements

Conflicts in Shift-Reduce Parsing

shift-reduce

a shift reduce conflict occurs when the grammar indicates that different successful parses might occur with either a shift or a reduce at a given point during parsing. The vast majority of situations where this conflict occurs can be correctly resolved by shifting.

reduce-reduce

a reduce reduce conflict occurs when the parser has two or more handles at the same time on the top of the stack. Whatever choice the parser makes is just as likely to be wrong as not. In this case it is usually best to rewrite the grammar to eliminate the conflict, possibly by factoring.

S->if E then S
S->if E then S else S

In many languages two nested "if" statements produce a situation where an "else" clause could legally belong to either "if". The usual rule (to shift) attaches the else to the nearest (i.e. inner) if statement.

Example reduce reduce conflict:

(1)	S -> id LP plist RP
(2)	S -> E GETS E
(3)	plist -> plist, p
(4)	plist -> p
(5)	p -> id
(6)	E -> id LP elist RP
(7)	E -> id
(8)	elist -> elist, E
(9)	elist -> E

Further Discussion of Reduce Reduce and Shift Reduce Conflicts

T : F | F T2 ;
T2 : p F T2 | ;
F : l T r | v ;

A slightly different grammar is needed to demonstrate a shift-reduce conflict:

T : F g;
T : F T2 g;
T2 : t F T2 ;
T2 : ;
F : l T r ;
F : v ;

The .output file generated by "bison -v" explains these conflicts in considerable detail. Part of what you need to interpret them are the concepts of "items" and "sets of items" discussed below.

YACC precedence and associativity declarations

%right ASSIGN
%left PLUS MINUS
%left TIMES DIVIDE
%right POWER
%%
expr: expr ASSIGN expr
    | expr PLUS expr
    | expr MINUS expr
    | expr TIMES expr
    | expr DIVIDE expr
    | expr POWER expr
    ;

• Use special predefined token error where errors expected
• On an error, the parser pops states until it enters one that has an action on the error token.
• For example: statement: error ';' ;
• The parser must see 3 good tokens before it decides it has recovered.
• yyerrok tells parser to skip the 3 token recovery rule
• yyclearin throws away the current (error-causing?) token
• yyerror(s) is called when a syntax error occurs (s is the error message)

Improving YACC's Error Reporting

You can easily add information in your own yyerror() function, for example GCC emits messages that look like:

goof.c:1: parse error before '}' token

void yyerror(char *s)
{
   fprintf(stderr, "%s:%d: %s before '%s' token\n",
	   yyfilename, yylineno, s, yytext);
}

You could instead, use the error recovery mechanism to produce better messages. For example

lbrace : LBRACE | { error_code=MISSING_LBRACE; } error ;

Another related option is to call yyerror() explicitly with a better message string, and tell the parser to recover explicitly:

package_declaration: PACKAGE_TK error
	{ yyerror("Missing name"); yyerrok; } ;

But, using error recovery to perform better error reporting runs against conventional wisdom that you should use error tokens very sparingly. What information from the parser determined we had an error in the first place? Can we use that information to produce a better error message?

LR Syntax Error Messages: Advanced Methods

Even just the parse state is enough to do pretty good error messages. yystate is not part of YACC's public interface, though, so you may have to play some tricks to pass it as a parameter into yyerror() from yyparse(). Say, for example:

#define yyerror(s) __yyerror(s,yystate)

A tool called Merr is available that let's you generate this yyerror function from examples: you supply the sample syntax errors and messages, and Merr figures out which parse state integer goes with which message. Merr also uses the yychar (current input token) to refine the diagnostics in the event that two of your example errors occur on the same parse state. See the Merr web page.

lecture #13 began here

Announcements

76, 74, 74, 74, 73, 72, 66, 65, 55, 52, 46, 35, 30, 30, 30, 15, 14

LR vs. LL vs. LR(0) vs. LR(1) vs. LALR(1)

LR Parsers

The LR parsing algorithm is given below.

ip = first symbol of input
repeat {
   s = state on top of parse stack
   a = *ip
   case action[s,a] of {
      SHIFT s': { push(a); push(s') }
      REDUCE A->beta: {
         pop 2*|beta| symbols; s' = new state on top
         push A
         push goto(s', A)
         }
      ACCEPT: return 0 /* success */
      ERROR: { error("syntax error", s, a); halt }
      }
   }

Constructing SLR Parsing Tables:

Definition: An LR(0) item of a grammar G is a production of G with a dot at some position of the RHS.

Example: The production A->aAb gives the items:

A -> . a A b
A -> a . A b
A -> a A . b
A -> a A b .

Note: A production A-> ε generates only one item:

A -> .

Intuition: an item A-> α . β denotes:

1. α - we have already seen a string derivable from α
2. β - we hope to see a string derivable from β

Functions on Sets of Items

Closure: if I is a set of items for a grammar G, then closure(I) is the set of items constructed as follows:

1. Every item in I is in closure(I).
2. If A->α . Bβ is in closure(I) and B->γ is a production, then add B-> .γ to closure(I).

These two rules are applied repeatedly until no new items can be added.

Intuition: If A -> α . B β is in closure(I) then we hope to see a string derivable from B in the input. So if B-> γ is a production, we should hope to see a string derivable from γ. Hence, B->.γ is in closure(I).

Goto: if I is a set of items and X is a grammar symbol, then goto(I,X) is defined to be:

goto(I,X) = closure({[A->αX.β] | [A->α.Xβ] is in I})

Intuition:

• [A->α.Xβ] is in I => we've seen a string derivable from α; we hope to see a string derivable from Xβ.
• Now suppose we see a string derivable from X
• Then, we should "goto" a state where we've seen a string derivable from αX, and where we hope to see a string derivable from β. The item corresponding to this is [A->αX.β]

• Example: Consider the grammar

	E -> E+T | T
	T -> T*F | F
	F -> (E) | id 

        goto(I,+) = closure({[E -> E+.T]})
		  = closure({[E -> E+.T], [E -> .T*F], [T -> .F]})
		  = closure({[E -> E+.T], [E -> .T*F], [T -> .F], [F-> .(E)], [F -> .id]})
		  = { [E -> E + .T],[T -> .T * F],[T -> .F],[F -> .(E)],[F -> .id]}

The Sets of Items Construction

1. Given a grammar G with start symbol S, construct the augmented grammar by adding a special production S'->S where S' does not appear in G.
2. Algorithm for constructing the canonical collection of LR(0) items for an augmented grammar G':

	begin
	   C := { closure({[S' -> .S]}) };
	   repeat
	      for each set of items I in C:
		  for each grammar symbol X:
   		     if goto(I,X) != 0 and goto(I,X) is not in C then
		 	 add goto(I,X) to C;
	   until no new sets of items can be added to C;
	   return C;
	end

Valid Items: an item A -> β ₁. β ₂ is valid for a viable prefix α β ₁ if there is a derivation:

S' =>*rm αAω =>*rmα β1β 2ω

Suppose A -> β₁.β ₂ is valid for αβ₁, and αB₁ is on the parsing stack

1. if β₂ != ε, we should shift
2. if β₂ = ε, A -> β₁ is the handle, and we should reduce by this production

Note: two valid items may tell us to do different things for the same viable prefix. Some of these conflicts can be resolved using lookahead on the input string.

Constructing an SLR Parsing Table

1. Given a grammar G, construct the augmented grammar by adding the production S' -> S.
2. Construct C = {I₀, I₁, … I_n}, the set of sets of LR(0) items for G'.
3. State I is constructed from I_i, with parsing action determined as follows:
   • [A -> α.aB] is in I_i, where a is a terminal; goto(I_i,a) = I_j : set action[i,a] = "shift j"
   • [A -> α.] is in I_i : set action[i,a] to "reduce A -> x" for all a e FOLLOW(A), where A != S'
   • [S' -> S] is in I_i : set action[i,$] to "accept"
4. goto transitions constructed as follows: for all non-terminals: if goto(I_i, A) = I_j, then goto[i,A] = j
5. All entries not defined by (3) & (4) are made "error". If there are any multiply defined entries, grammar is not SLR.
6. Initial state S₀ of parser: that constructed from I₀ or [S' -> S]

Example:

	S -> aABe		FIRST(S) = {a}		FOLLOW(S) = {$}
	A -> Abc		FIRST{A} = {b}		FOLLOW(A) = {b,d}
	A -> b			FIRST{B} = {d}		FOLLOW{B} = {e}
	B -> d			FIRST{S'}= {a}		FOLLOW{S'}= {$}
I0 = closure([S'->.S]
   = closure([S'->.S],[S->.aABe])
goto(I0,S) = closure([S'->S.]) = I1
goto(I0,a) = closure([S->a.Abe])
	    = closure([S->a.Abe],[A->.Abc],[A->.b]) = I2
goto(I2,A) = closure([S->aA.Be],[A->A.bc])
	    = closure([S->aA.Be],[A->A.bc],[B->.d]) = I3
goto(I2,B) = closure([A->b.]) = I4
goto(I3,B) = closure([S->aAB.e]) = I5
goto(I3,b) = closure([A->Ab.c]) = I6
goto(I3,d) = closure([B->d.]) = I7
goto(I5,e) = closure([S->aABe.]) = I8
goto(I6,c) = closure([A->Abc.]) = I9

lecture #14 began here

On Tree Traversals

Parse trees are k-ary, where there is a variable number of children bounded by a value k determined by the grammar. You may wish to consult your old data structures book, or look at some books from the library, to learn more about trees if you are not totally comfortable with them.

#include <stdarg.h>

struct tree {
   short label;			/* what production rule this came from */
   short nkids;			/* how many children it really has */
   struct tree *child[1];	/* array of children, size varies 0..k */
};

struct tree *alctree(int label, int nkids, ...)
{
   int i;
   va_list ap;
   struct tree *ptr = malloc(sizeof(struct tree) +
                             (nkids-1)*sizeof(struct tree *));
   if (ptr == NULL) {fprintf(stderr, "alctree out of memory\n"); exit(1); }
   ptr->label = label;
   ptr->nkids = nkids;
   va_start(ap, nkids);
   for(i=0; i < nkids; i++)
      ptr->child[i] = va_arg(ap, struct tree *);
   va_end(ap);
   return ptr;
}

Besides a function to allocate trees, you need to write one or more recursive functions to visit each node in the tree, either top to bottom (preorder), or bottom to top (postorder). You might do many different traversals on the tree in order to write a whole compiler: check types, generate machine- independent intermediate code, analyze the code to make it shorter, etc. You can write 4 or more different traversal functions, or you can write 1 traversal function that does different work at each node, determined by passing in a function pointer, to be called for each node.

void postorder(struct tree *t, void (*f)(struct tree *))
{
   /* postorder means visit each child, then do work at the parent */
   int i;
   if (t == NULL) return;

   /* visit each child */
   for (i=0; i < t-> nkids; i++)
      postorder(t->child[i], f);

   /* do work at parent */
   f(t);
}

void printer(struct tree *t)
{
   if (t == NULL) return;
   printf("%p: %d, %d children\n", t, t->label, t->nkids);
}

What we have at the start of semantic analysis is a syntax tree that corresponds to the source program as parsed using the context free grammar. Semantic information is added by annotating grammar symbols with semantic attributes, which are defined by semantic rules. A semantic rule is a specification of how to calculate a semantic attribute that is to be added to the parse tree.

So the input is a syntax tree...and the output is the same tree, only "fatter" in the sense that nodes carry more information. Another output of semantic analysis are error messages detecting many types of semantic errors.

Two typical examples of semantic analysis include:

variable reference analysis

the compiler must determine, for each use of a variable, which variable declaration corresponds to that use. This depends on the semantics of the source language being translated.

type checking

the compiler must determine, for each operation in the source code, the types of the operands and resulting value, if any.

Notations used in semantic analysis:

syntax-directed definitions

high-level (declarative) specifications of semantic rules

translation schemes

semantic rules and the order in which they get evaluated

In practice, attributes get stored in parse tree nodes, and the semantic rules are evaluated either (a) during parsing (for easy rules) or (b) during one or more (sub)tree traversals.

Two Types of Attributes:

synthesized

attributes computed from information contained within one's children. These are generally easy to compute, even on-the-fly during parsing.

inherited

attributes computed from information obtained from one's parent or siblings These are generally harder to compute. Compilers may be able to jump through hoops to compute some inherited attributes during parsing, but depending on the semantic rules this may not be possible in general. Compilers resort to tree traversals to move semantic information around the tree to where it will be used.

Attribute Examples

Isconst and Value

lecture #15 began here

Questions from the board and from the floor

Symbol Table Module

mktable(parent)

creates a new symbol table, whose scope is local to (or inside) parent

enter(table, symbolname, type, offset)

insert a symbol into a table

lookup(table, symbolname)

lookup a symbol in a table; returns structure pointer including type and offset. lookup operations are often chained together progressively from most local scope on out to global scope.

addwidth(table)

sums the widths of all entries in the table. ("widths" = #bytes, sum of widths = #bytes needed for an "activation record" or "global data section"). Worry not about this method until code generation you wish to implement.

enterproc(table, name, newtable)

enters the local scope of the named procedure

Variable Reference Analysis

• for each variable, has it been declared? (undeclared error)
• for each declaration, is it already declared? (redeclared error)

Reading Tree Leaves

Options:

1. encode in the parent what the types of children are
2. encode in each child what its own type is (better)

Perhaps the best approach to all this is to unify the tokens and parse tree nodes with something like the following, where perhaps an nkids value of -1 is treated as a flag that tells the reader to use lexical information instead of pointers to children:

struct node {
int code;		/* terminal or nonterminal symbol */
int nkids;
union {
   struct token { ...  } leaf;
   struct node *kids[9];
   }u;
} ;

Type Checking

Type Systems

• Base types (int, char, etc.) are types
• Named types (via typedef, etc.) are types
• Types composed using other types are types, for example:
  • array(T, indices) is a type. In some languages indices always start with 0, so array(T, size) works.
  • T1 x T2 is a type (specifying, more or less, the tuple or sequence T1 followed by T2; x is a so-called cross-product operator).
  • record((f1 x T1) x (f2 x T2) x ... x (fn x Tn)) is a type
  • in languages with pointers, pointer(T) is a type
  • (T₁ x ... T_n) -> T_n+1 is a type denoting a function mapping parameter types to a return type
• In some language type expressions may contain variables whose values are types.

lecture #16 began here

Midterm Exam Review

1. Write a regular expression for numeric quantities of U.S. money that start with a dollar sign, followed by one or more digits. Require a comma between every three digits, as in $7,321,212. Also, allow but do not require a decimal point followed by two digits at the end, as in $5.99
2. Use Thompson's construction to write a non-deterministic finite automaton for the following regular expression, an abstraction of the expression used for real number literal values in C.

        (d+pd*|d*pd+)(ed+)? 

3. Write a regular expression, or explain why you can't write a regular expression, for Modula-2 comments which use (* *) as their boundaries. Unlike C, Modula-2 comments may be nested, as in (* this is a (* nested *) comment *)
4. Write a context free grammar for the subset of C expressions that include identifiers and function calls with parameters. Parameters may themselves be function calls, as in f(g(x)), or h(a,b,i(j(k,l)))
5. What are the FIRST(E) and FOLLOW(T) in the grammar:

        E : E + T | T
        T : T * F | F
        F : ( E ) | ident

6. What is the ε-closure(move({2,4},b)) in the following NFA? That is, suppose you might be in either state 2 or 4 at the time you see a symbol b: what NFA states might you find yourself in after consuming b?
   (automata to be written on the board)

A: questions that allow you to demonstrate that you know the difference between an DFA and an NFA, questions about lex and flex and tokens and lexical attributes, questions about context free grammars: ambiguity, factoring, removing left recursion, etc.

On the mysterious TYPE_NAME

typedef int foo;
foo x;                    /* a normal use of typedef... */
foo foo;                  /* try this on gcc! is it a legal global? */
void main() { foo foo; }  /* what about this ? */

370-C does not support typedef's and without working typedef's the TYPE_NAME token simply will never occur. Typedef's are fair game for extra credit points.

Representing C (C++, Java, etc.) Types

struct c_type {
   int base_type;    /* 1 = int, 2=float, ... */
   union {
      struct array {
         int size;
	 struct c_type *elemtype;
      } a;
      struct ctype *p;
      struct struc {
         char *label;
         struct field **f;
	 } s;
   } u;
}

struct field {
   char *name;
   struct ctype *elemtype;
}

int [10][20]
struct foo { int x; char *s; }

Example Semantic Rules for Type Checking

Type Promotion and Type Equivalence

int x;
long y;
y = y + x;

For records/structures, some languages use name equivalence, while others use structure equivalence. Features like typedef complicate matters. If you have a new type name MY_INT that is defined to be an int, is it compatible to pass as a parameter to a function that expects regular int's? Object-oriented languages also get interesting during type checking, since subclasses usually are allowed anyplace their superclass would be allowed.

Implementing Structs

1. storing and retrieving structs by their label -- the struct label is how structs are identified. You do not have to do typedefs and such. The labels can be keys in a separate hash table, similar to the global symbol table. You can put them in the global symbol table so long as you can tell the difference between them and variable names.
2. You have to store fieldnames and their types, from where the struct is declared. You could use a hash table for each struct, but a link list is OK as an alternative.
3. You have to use the struct information to check the validity of each dot operator like in rec.foo. To do this you'll have to lookup rec in the symbol table, where you store rec's type. rec's type must be a struct type for the dot to be legal, and that struct type should include a hash table or link list that gives the names and types of the fields -- where you can lookup the name foo to find its type.

lecture #17 began here

Run-time Environments

• Relationship between source code names and data objects during execution
• Procedure activations
• Memory management and layout
• Library functions

lecture #18 began here

Announcements

• Affinity Research Group Workshop this Saturday, 9-3 in SH 124. Extra credit: 20 points will be added to your midterm exam grade for attending and providing sincere attention at this workshop. Lunch is also provided.
• HW#5 is available

Scopes and Bindings

Scope rules for each language determine how to go from names to declarations.

Each use of a variable name must be associated with a declaration. This is generally done via a symbol table. In most compiled languages it happens at compile time (in contrast, for example ,with LISP).

Environment and State

Runtime Memory Regions

Questions to ask about a language, before writing its code generator

1. May procedures be recursive? (Duh, all modern languages...)
2. What happens to locals when a procedure returns? (Lazy deallocation rare)
3. May a procedure refer to non-local, non-global names? (Pascal-style nested procedures, and object field names)
4. How are parameters passed? (Many styles possible, different declarations for each (Pascal), rules hardwired by type (C)?)
5. May procedures be passed as parameters? (Not too awful)
6. May procedures be return values? (Adds complexity for non-local names)
7. May storage be allocated dynamically (Duh, all modern languages... but some languages do it with syntax (new) others with library (malloc))
8. Must storage by deallocated explicitly (garbage collector?)

Activation Records

"Modern" Runtime Systems

• Garbage collection. Automatic storage management plays a prominent role in most modern languages; it is one of the single most important features that makes programming easier.

  The Basic problem in garbage collection: given a piece of memory, are there any pointers to it? (And if so, where exactly are all of them please). Approaches:

  • reference counting
  • traversal of known pointers (marking)
    • copying (2 heaps approach)
    • compacting (mark and sweep)
    • generational
  • conservative collection
• Reflection. Modern languages' values can often describe themselves. This plays a central role in Visual GUI builders and Visual IDE's, component architectures and other uses.
• Just-in-time compilation. Modern languages often have a virtual machine model...and a compiler built-in to the VM that converts VM instructions to native code for frequently executed methods or code blocks.
• Security model. Modern languages may attempt to guarantee certain security properties, or prevent certain kinds of attacks.

Having Trouble Debugging?

To work on segmentation faults: recompile all .c files with -g and run your program inside gdb to the point of the segmentation fault. Type the gdb "where" command. Print the values of variables on the line mentioned in the debugger as the point of failure. If it is inside a C library function, use the "up" command until you are back in your own code, and then print the values of all variables mentioned on that line.

There is one more tool you should know about, which is useful for certain kinds of bugs, primarily subtle memory violations. It is called electric fence. To use electric fence you add

	/home/uni1/jeffery/ef/ElectricFence-2.1/libefence.a

lecture #19 began here

Need Help with Type Checking?

• Implement the C Type Representation given in lecture #16.
• Read the Book
• What OPERATIONS (functions) do you need, in order to check whether types are correct? What parameters will they take?

Can be formulated as syntax-directed translation

• add new attributes where necessary, e.g. for expression E we might have

  E.place

  the name that holds the value of E

  E.code

  the sequence of intermediate code statements evaluating E.

• new helper functions, e.g.

  newtemp()

  returns a new temporary variable each time it is called

  newlabel()

  returns a new label each time it is called

• actions that generate intermediate code formulated as semantic rules

• translate easily into real machine code
• form a linearized representation of a syntax tree
• allow us to check our own work to this point
• allow machine independent code optimizations to be performed
• increase the portability of the compiler

Instruction set:

mnemonic	C equivalent	description
ADD, SUB,MUL,DIV	x := y op z	store result of binary operation on y and z to x
NEG	x := op y	store result of unary operation on y to x
ASN	x := y	store y to x
ADDR	x := &y	store address of y to x
LCONT	x := *y	store contents pointed to by y to x
SCONT	*x := y	store y to location pointed to by x
GOTO	goto L	unconditional jump to L
BLESS,...	if x rop y then goto L	binary conditional jump to L
BIF	if x then goto L	unary conditional jump to L
BNIF	if !x then goto L	unary negative conditional jump to L
PARM	param x	store x as a parameter
CALL	call p,n,x	call procedure p with n parameters, store result in x
RET	return x	return from procedure, use x as the result

Declarations (Pseudo instructions): These declarations list size units as "bytes"; in a uniform-size environment offsets and counts could be given in units of "slots", where a slot (4 bytes on 32-bit machines) holds anything.

global x,n1,n2	declare a global named x at offset n1 having n2 bytes of space
proc x,n1,n2	declare a procedure named x with n1 bytes of parameter space and n2 bytes of local variable space
local x,n	declare a local named x at offset n from the procedure frame
label Ln	designate that label Ln refers to the next instruction
end	declare the end of the current procedure

TAC Adaptations for Object Oriented Code

x := y field z	lookup field named z within y, store address to x
class x,n1,n2	declare a class named x with n1 bytes of class variables and n2 bytes of class method pointers
field x,n	declare a field named x at offset n in the class frame
new x	create a new instance of class name x

Variable Allocation and Access Issues

globals

easy, symbol table lookup

locals

easy, symbol table gives offset in (current) activation record

objects

easy, symbol table gives offset in object, activation record has pointer to object in a standard location

locals in some enclosing block/method/procedure

ugh. Pascal, Ada, and friends offer their own unique kind of pain. Q: does the current block support recursion? Example: for procedures the answer would be yes; for nested { { } } blocks in C the answer would be no.

• if no recursion, just count back some number of frame pointers based on source code nesting
• if recursion, you need an extra pointer field in activation record to keep track of the "static link", follow static link back some # of times to find a name defined in an enclosing scope

Sizing up your Regions and Activation Records

• The size of integers is 4 (for x86; varies by CPU).
  
• The size of reals is... ? (for x86; varies by CPU).
  
• The size of strings is... <= 256? You could allocate static 256 character arrays in the global area, but better to do them as a descriptor consisting of a length and a pointer.
  
• The size of arrays is (sizeof (struct descrip)) * the number of elements? Do we know an array size?
• Are arrays all int, or all real, or can they be mixed? (in BASIC and other dynamic languages, they can be mixed!)
• Are there arrays of strings? -- yes
• what about sizes of structs?

You do this sizing up once for each scope. The size of each scope is the sum of the sizes of symbols in its symbol table.

Run Time Type Information

struct descrip {
   short type;
   short size;
   union {
      char *string;
      int ival;
      float rval;
      struct descrip *array;
      /* ... for other types */
      } value;
   };

Compute the Offset of Each Variable

Locals and Parameters are not Contiguous

Basic Blocks

What are the basic blocks in the following 3-address code? ("read" is a 3-address code to read in an integer.)

	read x
	t1 = x > 0
	if t1 == 0 goto L1
	fact = 1
	label L2
	t2 = fact * x
	fact = t2
	t3 = x - 1
	x = t3
	t4 = x == 0
	if t4 == 0 goto L2
	t5 = addr const:0
	param t5		; "%d\n"
	param fact
	call p,2
	label L1
	halt

Intermediate Code for Control Flow

Depending on your source language's semantic rules for things like "short-circuit" evaluation for boolean operators, the operators like || and && might be similar to + and * (non-short-circuit) or they might be more like if-then code.

A general technique for implementing control flow code is to add new attributes to tree nodes to hold labels that denote the possible targets of jumps. The labels in question are sort of analogous to FIRST and FOLLOW; for any given list of instructions corresponding to a given tree node, we might want a .first attribute to hold the label for the beginning of the list, and a .follow attribute to hold the label for the next instruction that comes after the list of instructions. The .first attribute can be easily synthesized. The .follow attribute must be inherited from a sibling. The labels have to actually be allocated and attached to instructions at appropriate nodes in the tree corresponding to grammar production rules that govern control flow. An instruction in the middle of a basic block need neither a first nor a follow.

C code	Attribute Manipulations
S->if E then S1	E.true = newlabel(); E.false = S.follow; S1.follow = S.follow; S.code = E.code || gen(LABEL, E.true)|| S1.code
S->if E then S1 else S2	E.true = newlabel(); E.false = newlabel(); S1.follow = S.follow; S2.follow = S.follow; S.code = E.code || gen(LABEL, E.true)|| S1.code || gen(GOTO, S.follow) || gen(LABEL, E.false) || S2.code

Exercise: OK, so what does a while loop look like?

lecture #20 began here

Announcement

LANL is seeking outstanding SOPHOMORE, JUNIOR AND NON- GRADUATING SENIOR LEVEL Computer Science majors to work in the areas of networking, desktop support, high performance computing or software engineering. Positions are available for the fall 2006 semester. MUST HAVE A GPA OF 3.0 OR HIGHER.

To request a referral go to www.nmsu.edu/pment, click on "Co- op Job Listings", Job #86 or call the co-op office at 646- 4115. LANL is requiring a cover letter to also be sent, please send that via email at coop@nmsu.edu in the subject line put attn: LANL cover letter.

Co-op Office 646-4115

More on Generating Code for Boolean Expressions

Comparing Regular and Short Circuit Control Flow

Implementation techniques for these alternatives include:

1. treat boolean operators same as arithmetic operators, evaluate each and every one into temporary variable locations.
2. add extra attributes to keep track of code locations that are targets of jumps. The attributes store link lists of those instructions that are targets to backpatch once a destination label is known. Boolean expressions' results evaluate to jump instructions and program counter values (where you get to in the code implies what the boolean expression results were).
3. one could change the machine execution model so it implicity routes control from expression failure to the appropriate location. In order to do this one would
   • mark boundaries of code in which failure propagates
   • maintain a stack of such marked "expression frames"

Non-short Circuit Example

a<b || c<d && e<f

100:	if a<b goto 103
	t1 = 0
	goto 104
103:	t1 = 1
104:	if c<d goto 107
	t2 = 0
	goto 108
107:	t2 = 1
108:	if e<f goto 111
	t3 = 0
	goto 112
111:	t3 = 1
112:	t4 = t2 AND t3
	t5 = t1 OR t4

Short-Circuit Example

a<b || c<d && e<f

	if a<b goto L1
	if c<d goto L2
	goto L3
L2:	if e<f goto L1
L3:	t = 0
	goto L4
L1:	t = 1
L4:	...

While Loops

lecture #21 began here

Intermediate Code Generation Examples

void main()
{
   int i;
   i = 0;
   while (i < 20)
      i = i * i + 1;
   print(i);
}

Intermediate Code Generation Example (cont'd)

   i = 0;
   if (i >= 20) goto L50;
   i = i * i + 1;
   goto 20;
   print(i);

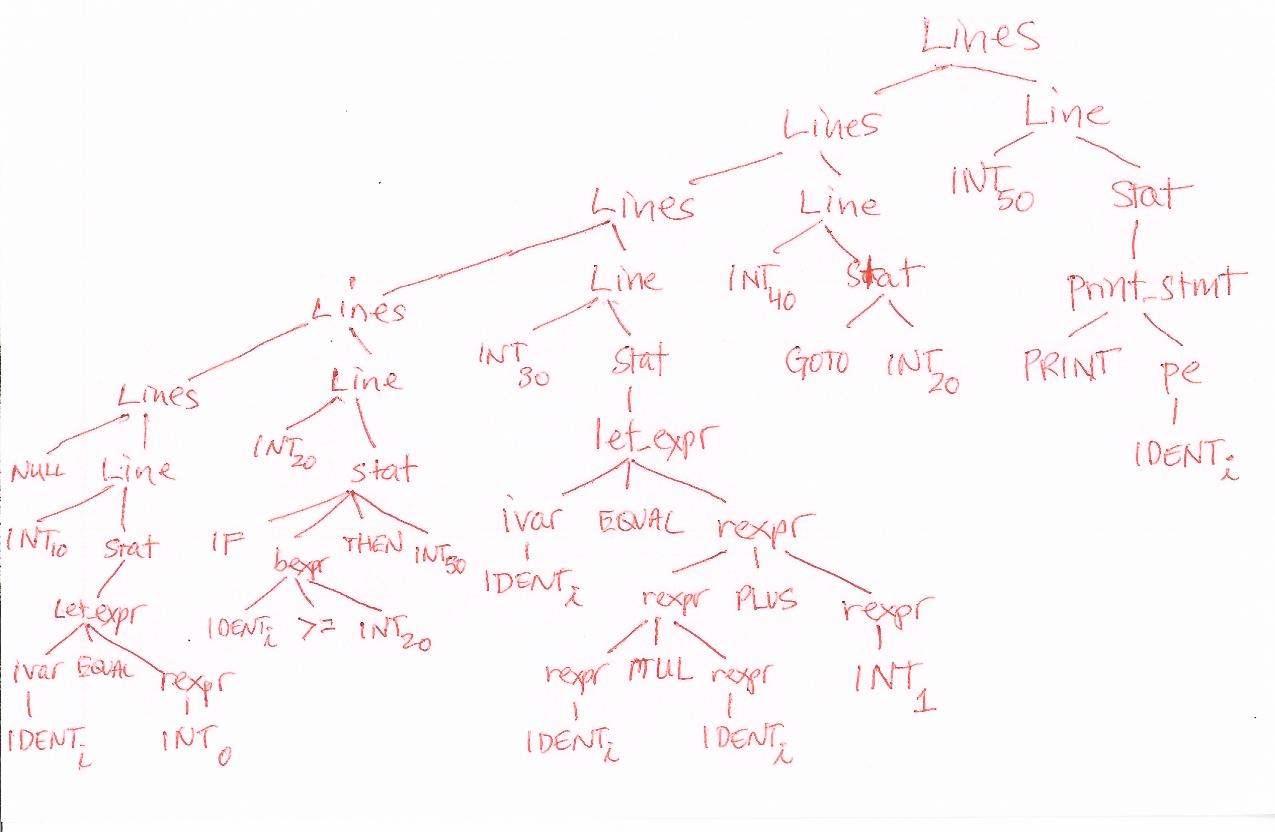A syntax tree, with attributes obtained from lexical and semantic analysis, needs to be shown here. During semantic analysis, it is discovered that "print" has not been defined, so let it be:

void print(int i) { }

The code for the boolean conditional expression controlling the while loop is a list of length 1, containing the instruction t0 = i < 20, or more formally

opcode	dest	src1	src2
LT	t0	i	20

The actual C representation of addresses dest, src1, and src2 is probably as a

region offset

pair, so the picture of this intermediate code instruction really looks something like this:

opcode	dest	src1	src2
LT	local t0.offset	local i.offset	const 20

Regions are expressed with a simple integer encoding like: global=1, local=2, const=3. Note that address values in all regions are offsets from the start of the region, except for region "const", which stores the actual value of a single integer as its offset.

opcode	dest	src1	src2
MUL	local t1.offset	local i.offset	local i.offset

lecture #22 began here

Comments on Trees and Attributes

Traversal code example

void codegen(nodeptr t)
{
   int i, j;
   if (t==NULL) return;

   /*
    * this is a post-order traversal, so visit children first
    */
   for(i=0;i<t->nkids;i++)
      codegen(t->child[i]);

   /*
    * back from children, consider what we have to do with
    * this node. The main thing we have to do, one way or
    * another, is assign t->code
    */
   switch (t->label) {
   case PLUS: {
      t->code = concat(t->child[0].code, t->child[1].code);
      g = gen(PLUS, t->address,
              t->child[0].address, t->child[1].address);
      t->code = concat(t->code, g);
      break;
      }
   /* ... really, we need a bazillion cases, perhaps one for each
    * production rule (in the worst case)
    */
   default:
      /* default is: concatenate our children's code */
      t->code = NULL;
      for(i=0;i<t->nkids;i++)
         t->code = concat(t->code, t->child[i].code);
   }
}

Code generation examples

Zero operators.

if (x) S

if x != 0 goto L1
goto L2
label L1
...code for S
label L2

if x == b goto L1
...code for S
label L1

One relational operator.

if (a < b) S

if i >= b goto L1
...code for S
label L1

if (a < b  &&  c > d) S

if (a < b)
   if (c > d)
      ...code for S

if i >= b goto L1
if c <= d goto L2
...code for S
label L2
label L1

if (a < b  ||  c > d) S

if (a < b) ...code for S
if (c > d) ...code for S

if a < b goto L1
if c > d goto L2
goto L3
label L2
label L1
...code for S
label L3

Array subscripting!

now, what about arrays? reading an array value: x = a[i]. Draw the picture. Consider the machine uses byte-addressing, not word-addressing.

t0 := addr a
t1 := i * 4
t2 := plus t0 t1
t3 := deref t2
x  := t3

Debugging Miscellany

makefile .h dependencies!

if you do not list makefile dependencies for important .h files, you may get coredumps!

traversing multiple times by accident?

at least in my version, I found it easy to accidentally re-traverse portions of the tree. this usually had a bad effect.

bad grammar?

our sample grammar was adapted from good sources, but don't assume its impossible that it could have a flaw or that you might have messed it up.

lecture #23 began here

Remind me to come back to HW #6 before the end of today's lecture.

Final Code

Alternatives:

interpret the source code

we could have build an interpreter instead of a compiler, in which the source code was kept in string or token form, and re-parsed every execution. Early BASIC's did this, but it is Really Slow.

interpret the parse tree

we could have written an interpreter that executes the program by walking around on the tree doing traversals of various subtrees. This is still slow, but successfully used by many "scripting languages".

interpret the 3-address code

we could interpret the link-list or a more compact binary representation of the intermediate code

translate into VM instructions

popular virtual machines such as JVM or .Net allow execution from an instruction set that is often higher level than hardware, may be independent of the underlying hardware, and may be oriented toward supporting the specific language features of our source language. For example, there are various BASIC virtual machines out there.

translate into "native" instructions

"native" generally means hardware instructions.

Collecting Information Necessary for Final Code Generation

• a top-down approach to learning your native target code is to study a reference work supplied by the chip manufacturer, such as the Intel 80386 Programmer's Reference Manual
• a bottom-up approach to learning your native target code is to study an existing compiler's native code. For example, running "gcc -S foo.c" will compile foo.c into a human-readable native assembler code equivalent foo.s file which you can examine. By systematically studying .s files for various toy C programs you can learn native instructions corresponding to each C construct, including ones equivalent to the various 3-address instructions.

Instruction Selection

Register Allocation and Assignment

In the Old Days, there were Load-Store hardware architectures in which only one (accumulator) register was present. On such an architecture, register allocation and assignment is not needed; the compiler has few options about how it uses the accumulator register. Traditional x86 16-bit architecture was only a little better than a load-store architecture, with 4 registers instead of 1. At the other extreme, Recent History has included CPU's with 32 or more general purpose registers. On such systems, high quality compiler register allocation and assignment makes a huge difference in program execution speed. Unfortunately, optimal register allocation and assignment is NP-complete, so compilers must settle for doing a "good" job.

Discussion of Tree Traversals that perform Semantic Tests.

AssignStmt : Var EQU Expr.

AssignStmt : Var EQU Expr { $$ = alctree(..., $1, $2, $3);
	lvalue($1);
	rvalue($3);
	}

void lvalue(struct tree *t)
{
   if (t->label == IDENT) {
      struct symtabentry *ste = lookup(t->u.token.name);
      ste->lvalue = 1;
   }
   for (i=0; inkids; i++) {
      lvalue(t->child[i]);
      }
}
void rvalue(struct tree *t)
{
   if (t->label == IDENT) {
      struct symtabentry *ste = lookup(t->u.token.name);
      if (ste->lvalue == 0) warn("possible use before assignment");
   }
   for (i=0; inkids; i++) {
      lvalue(t->child[i]);
      }
}

What is different about real life as opposed to this toy example

lecture #24 began here

Runtime Systems

So you need a runtime system; potentially, this might be as big or bigger a job than writing the compiler. Languages vary from assembler (no runtime system) and C (small runtime system, mostly C with some assembler) on up to Java (large runtime system, mostly Java with some C) and in even higher level languages the compiler may evaporate and the runtime system become gigantic. The Unicon language has a relatively trivial compiler and gigantic virtual machine and runtime system. Other scripting languages might have no compiler at all, doing everything (even lexing and parsing) in the runtime system.

For your project: whether you generate C or X86 or Java, you'll need a plan for what to do about a runtime system. And, in principle, I am not opposed to helping with this part. But the compiler and runtime system have to fit together; if I write part of the BASIC runtime system for you, or we write it together, we have to agree on things such as: what the types of parameters and return values must look like.

So, what belongs in a Color BASIC runtime system? Anything not covered by a three address instruction. Looking at cocogram.y:

• INPUT/PRINT
• READ/DATA
• CLEAR
• CLOAD/CSAVE/SKIPF
• CLS
• SET/RESET
• SOUND
• CHR$, LEFT$, MID$, RIGHT$, INKEY$
• ASC, INT, JOYSTK, LEN, PEEK, RND, VAL
• DIM
• string +, string compares

What would a runtime system function look like? It would take in and pass out BASIC values, represented as C structs. You would then link this code in to your generated C or assembler code (if you generated Java code, you would have to deal with the Java Native Interface or else write these functions in Java).

void PRINT(struct descrip *d)
{
   switch (d->type) {
   case INTEGER: printf("%d",d->value.ival); break;
   case REAL: printf("%f",d->value.rval); break;
   case STRING: printf("%*s",d->size,d->value.string); break;
   case ARRAY: printf("cannot print arrays"); break; /* can't get here */
   default: printf("PRINT: internal error, type %d\n", d->type);
   }
}

• libb.c

More on Memory Management in the BASIC Runtime System

What do variables A, A(), A$, and A$() look like in memory? How does our runtime system make it so?

Let's take a look at DIM, in libc.c. This DIM is for arrays of numbers. How would you handle arrays of strings?

Can you implement STRCAT for your BASIC runtime system?

What other BASIC statements, operators, or functions allocate memory?

How would we avoid memory "leaks"?

Final Project comments

• We have a week of classes more, plus a couple weekends, before your final project (HW#7) is due.
• Really, really, test your turnin, by "turning your .tar in to yourself": unpacking in a separate directly, and verifying that it builds and runs correctly in a separate subdirectory. Turnins that do not compile and run due to missing files, etc. may receive a 0.
• You are invited and encouraged, but not required, to make an appointment to demo your compiler with me during Finals week. The purpose is to make sure you get credit for those parts which you can show me are working (as opposed to me testing your program independently and somehow missing the parts that work).
• Student assignments which have "impossible similarity" to each other may result in a 0 for the assignment or an "F" for the course. Impossible similarity means: beyond a reasonable doubt, substantial code other than sample code fragments provided in lecture or lab notes, has been shared or copied.

STRCAT

GOSUBs

If you use the "call" (3-address) instruction to do GOSUB, your native code will have to make a clear distinction between BASIC call's and calls to runtime system (built-in) functions. Perhaps it is best to implement BASIC GOSUB by pushing a "param" (the next instruction following the GOSUB) and a "goto". The BASIC RETURN is then a "pop" followed by a "goto". What, we don't have a "pop" 3-address instruction? We do now... the name of "param" should probably be "push" anyhow.

Come to think of it, we've been talking about doing a call to a built-in function such as PRINT, but that PRINT function we wrote is C code; it doesn't do a 3-address "ret" instruction, hmmm. How are we going to generate the native code for the 3-address "call" instruction? It may include an assembler call instruction, but it may also involve instructions to handle the interface between BASIC and C.

lecture #25 began here

Register Allocation and Assignment (cont'd)

Even if an instruction set does support memory-based operations, most compilers will want to load load a value into a register while it is being used, and then spill it back out to main memory when the register is needed for another purpose. The task of minimizing memory accesses becomes the task of minimizing register loads and spills.

Some Code Generation Examples

Reusing a Register

   a = a+b+c+d+e+f+g+a+c+e;

	movl	b, %eax
	addl	a, %eax
	addl	c, %eax
	addl	d, %eax
	addl	e, %eax
	addl	f, %eax
	addl	g, %eax
	addl	a, %eax
	addl	c, %eax
	addl	e, %eax
	movl	%eax, a

   a = (a+b)*(c+d)*(e+f)*(g+a)*(c+e);

	movl	b, %eax
	movl	a, %edx
	addl	%eax, %edx
	movl	d, %eax
	addl	c, %eax
	imull	%eax, %edx
	movl	f, %eax
	addl	e, %eax
	imull	%eax, %edx
	movl	a, %eax
	addl	g, %eax
	imull	%eax, %edx
	movl	e, %eax
	addl	c, %eax
	imull	%edx, %eax
	movl	%eax, a

   a = ((a+b)*(c+d))+((e+f)*(g+a))+(c*e);

	movl	b, %eax
	movl	a, %edx
	addl	%eax, %edx
	movl	d, %eax
	addl	c, %eax
	movl	%edx, %ecx
	imull	%eax, %ecx
	movl	f, %eax
	movl	e, %edx
	addl	%eax, %edx
	movl	a, %eax
	addl	g, %eax
	imull	%edx, %eax
	leal	(%eax,%ecx), %edx
	movl	c, %eax
	imull	e, %eax
	leal	(%eax,%edx), %eax
	movl	%eax, a

   a = ((a+b)*(c+d))+(((e+f)*(g+a))/(c*e));

	movl	b, %eax
	movl	a, %edx
	addl	%eax, %edx
	movl	d, %eax
	addl	c, %eax
	movl	%edx, %ecx
	imull	%eax, %ecx
	movl	f, %eax
	movl	e, %edx
	addl	%eax, %edx
	movl	a, %eax
	addl	g, %eax
	imull	%eax, %edx
	movl	c, %eax
	imull	e, %eax
	movl	%eax, -4(%ebp)
	movl	%edx, %eax
	cltd
	idivl	-4(%ebp)
	movl	%eax, -4(%ebp)
	movl	-4(%ebp), %edx
	leal	(%edx,%ecx), %eax
	movl	%eax, a

Code Generation for Virtual Machines

no registers, simplified addressing

a virtual machine may omit a register model and avoid complex addressing modes for different types of variables

uni-size or descriptor-based values

if all variables are "the same size", some of the details of memory management are simplified. In Java most values occupy a standard "slot" size, although some values occupy two slots. In Icon and Unicon, all values are stored using a same-size descriptor.

runtime type system

requiring type information at runtime may complicate the code generation task since type information must be present in generated code. For example in Java method invocation and field access instructions must encode class information.

	iload_1
	iload_2
	iadd
	iload_3
	iload 4
	iadd
	imul
	iload 5
	iload 6
	iadd
	iload 7
	iload_1
	iadd
	imul
	iload_3
	iload 5
	imul
	idiv
	iadd
	istore_1

lecture #26 began here

A Shallow Introduction to Code Optimization

Peephole Optimization

name	sample	optimized as
redundant load or store	MOVE R0,a MOVE a,R0	MOVE R0,a
dead code	#define debug 0 ... if (debug) printf("ugh");
control flow simplification	if a < b goto L1 ... L1: goto L2	if a < b goto L2 ... L1: goto L2
algebraic simplification	x = x * 1;
strength reduction	x = y * 16;	x = y << 4;

Constant Folding

     x = 7;
     ...
     y = x+5;

Common Subexpression Elimination

Explicit:

    (a+b)*i + (a+b)/j;

Implicit:

    x = a[i]; a[i] = a[j]; a[j] = x;

Loop Unrolling

for(i=0; i<3; i++) {
   x += i * i;
   y += x * x;
   }

   x += 0 * 0;
   y += x * x;
   x += 1 * 1;
   y += x * x;
   x += 2 * 2;
   y += x * x;

   y += x * x;
   x += 1;
   y += x * x;
   x += 4;
   y += x * x;

Hoisting Loop Invariants

for (i=0; i<strlen(s); i++)
   s[i] = tolower(s[i]);

t_0 = strlen(s);
for (i=0; i<t_0; i++)
   s[i] = tolower(s[i]);

Interprocedural Optimization

argument culling

f(x,r,s,1);

int f(int x, float y, char *z, int n)
{
  switch (n) {
  case 1:
     do_A; break;
  case 2:
     do_B; break;
     ...
     }
}

f_1(x,r,s);

int f_1(int x, float y, char *z)
{
   do_A;
}
int f_2(int x, float y, char *z)
{
   do_B;
}
...

Final Exam Review

• Review your lexical analysis, regular expressions, and finite automata.
• Review your syntax analysis, CFG's, and parsing.
• If a parser discovers a syntax error, how can it report what line number that error occurs on? If semantic analysis discovers a semantic error (or probable semantic error), how can it report what line number that error occurs on?
• What are symbol tables?
• What are symbol tables used for? What information is stored there?
• How does information get into a symbol table?
• How many symbol tables does a compiler need?
• What is "semantic analysis"?
• What does "semantic analysis" accomplish? What are its side effects?
• What are the primary activities of a compiler's semantic analyzer?
• What are memory regions, and why does a compiler care?
• What memory regions are there, and how do they affect code generation?
• What does code generation do, anyhow?
• What kinds of code generation are there?
• Why do (almost all) compilers use an "intermediate code"? What does intermediate code look like? How is it different from final code?